Домой | Мысли | Физ-мат Мысли | Наверх.
> restart:with(plots):interface(showassumed=0);
Warning, the name changecoords has been redefined
Преобразования координат
В данном файле рассмотрено движение Наблюдателя и его Собаки в инерциальной и неинерциальной системах отсчета (СО) с применением общей теории относительности
С точки зрения неподвижной СО Наблюдатель вращается по кругу некоторого радиуса R с некоторой угловой скоростью w, что дает касательную скорость вращения v = R*w.
В неинерциальной системе отсчета Наблюдателя - он покоится. И для измерения длины окружности пускает вдоль нее свою Собаку, с небольшой линейной скоростью u. Засекая время, за которое собака сделает полный оборот и вернется к нему, и умножая это время на скорость, Наблюдатель судит о длине окружности в его СО.
Рассмотрение данного опыта с точки зрения неподвижной СО с использованием специальной теории относительности почему-то приводит к противоречиям.
t,r,a,z - координаты во вращающейся СО
t1,x,y,z1 - координаты в неподвижной СО
w - угловая скорость вращения первой СО с точки зрения второй
линейная скорость заивисит от радиуса
> v:=r*w;
![]()
преобразование времени зависит от линейной скорости и т.о. от радиуса
> t1:=t/sqrt(1-v^2/c^2);
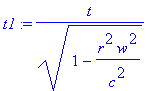
преобразование, дающее координату x
> x:=r*cos(a+w*t1);
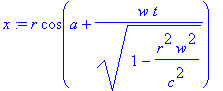
преобразование, дающее координату y (у)
> y:=r*sin(a+w*t1);
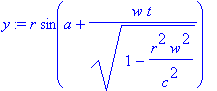
преобразование, дающее координату z1
> z1:=z;
![]()
> unassign('v');
Проверка: путь Наблюдателя и Собачки
Для проверки посмотрим, как заданные мировые линии во вращающейся СО выглядят в неподвижной
Наблюдатель
Координаты Наблюдателя во вращающейся СО равны (t,R,0,0) то есть он покоится на расстоянии R от начала координат, на начале отсчета полярного угла, в плоскости z=0
> t_obs := t; r_obs := R; a_obs := 0; z_obs := 0;
![]()
![]()
![]()
![]()
Координаты Наблюдателя в неподвижной СО получаются при помощи преобразований, заданных выше
> x_obs := subs({t=t_obs,r=r_obs,a=a_obs,z=z_obs,w=v/R},x); y_obs := subs({t=t_obs,r=r_obs,a=a_obs,z=z_obs,w=v/R},y); z1_obs := subs({t=t_obs,r=r_obs,a=a_obs,z=z_obs,w=v/R},z1); t1_obs := subs({t=t_obs,r=r_obs,a=a_obs,z=z_obs,w=v/R},t1);
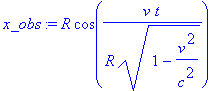
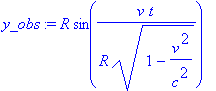
![]()
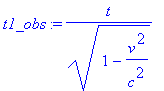
Для образца зададим значения скоростей, которые будут использованы при построении графиков
> c_sam := 300000; R_sam := 10000; v_sam := 100000; u_sam := 0.5;
![]()
![]()
![]()
![]()
На графике движение в координатах неподвижной СО видно, что это чистая окружность (параметр варьирован не до конца)
> TRA_obs:=plot([subs({R=R_sam,v=v_sam,c=c_sam},x_obs),subs({R=R_sam,v=v_sam,c=c_sam},y_obs),t=0..0.5],scaling=CONSTRAINED,axes=BOXED,color=blue):display(TRA_obs);
![[Maple Plot]](images/dog4a18.gif)
Для вычисления продольной скорости Наблюдателя в неподвижной СО рассчитаем дифференциалы смещений по координатам и дифференциал времени
> dx_obs:=diff(x_obs,t)*dt; dy_obs := diff(y_obs,t)*dt; dt_obs := diff(t1_obs,t)*dt;
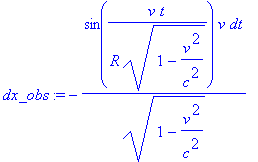
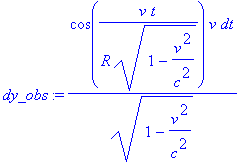
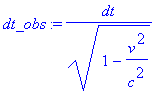
Затем составляющие вектора скорости как частные дифференциалов и получим длину вектора
> assume(u>0,v>0,v<c); vx_obs:=dx_obs/dt_obs; vy_obs:=dy_obs/dt_obs; v_obs:=simplify(sqrt(vx_obs^2 + vy_obs^2));
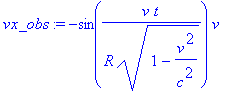
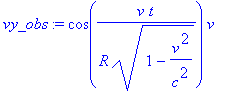
![]()
Вышеприведенные расчеты показывают, что с точки зрения неподвижной СО Наблюдатель действительно выполняет вращение по окружности с линейной скоростью w*R = v
Собака
Координаты Собаки в СО Наблюдателя меняются так, что она движется с постоянной скоростью u по окружности
> t_dog := t; r_dog := R; a_dog := u*t/R; z_dog := 0;
![]()
![]()
![]()
![]()
> x_dog := subs({t=t_dog,r=r_dog,a=a_dog,z=z_dog,w=v/R},x); y_dog := subs({t=t_dog,r=r_dog,a=a_dog,z=z_dog,w=v/R},y); z1_dog := subs({t=t_dog,r=r_dog,a=a_dog,z=z_dog,w=v/R},z1); t1_dog := subs({t=t_dog,r=r_dog,a=a_dog,z=z_dog,w=v/R},t1);
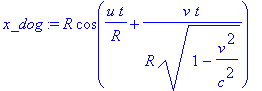
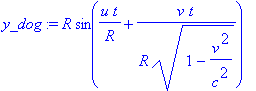
![]()
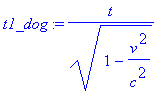
На графике движение в координатах неподвижной СО видно, что это чистая окружность (параметр варьирован не до конца)
> TRA_dog:=plot([subs({R=R_sam,v=v_sam,u=u_sam,c=c_sam},x_dog),subs({R=R_sam,v=v_sam,u=u_sam,c=c_sam},y_dog),t=0..0.5],scaling=CONSTRAINED,axes=BOXED,color=green): display(TRA_dog);
![[Maple Plot]](images/dog4a33.gif)
Для вычисления продольной скорости Собаки в неподвижной СО рассчитаем дифференциалы смещений по координатам и дифференциал времени
> dx_dog:=diff(x_dog,t)*dt; dy_dog := diff(y_dog,t)*dt; dt_dog := diff(t1_dog,t)*dt;
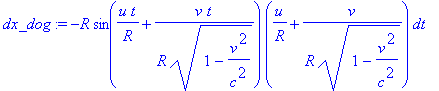
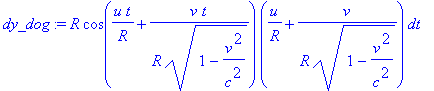
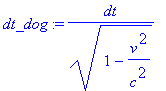
Затем составляющие вектора скорости как частные дифференциалов и получим длину вектора
> assume(u>0,v>0,v<c,u<v); vx_dog:=dx_dog/dt_dog; vy_dog:=dy_dog/dt_dog; v_dog:=simplify(sqrt(vx_dog^2 + vy_dog^2));
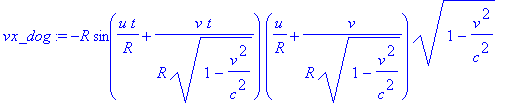
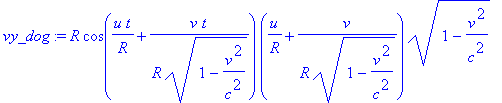
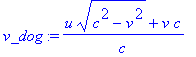
Дифференциалы преобразования координат
> assume(r>0,r<c/w,c>0,w>0);
Дифференциал преобразования времени
> dt1:=diff(t1,a)*da + diff(t1,r)*dr + diff(t1,t)*dt + diff(t1,z)*dz;
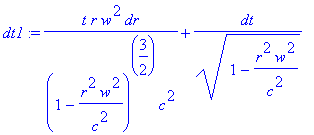
Дифференциал преобразования координаты x
> dx:=diff(x,a)*da + diff(x,r)*dr + diff(x,t)*dt + diff(x,z)*dz;
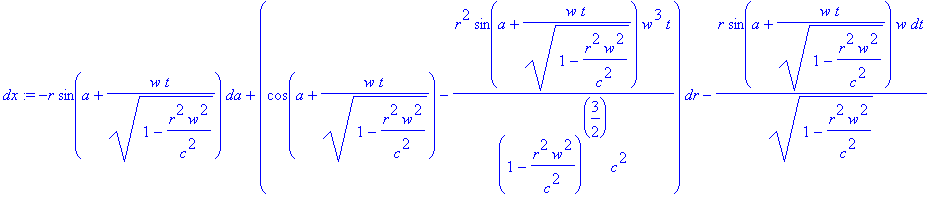
Дифференциал преобразования координаты y
> dy:=diff(y,a)*da + diff(y,r)*dr + diff(y,t)*dt + diff(y,z)*dz;
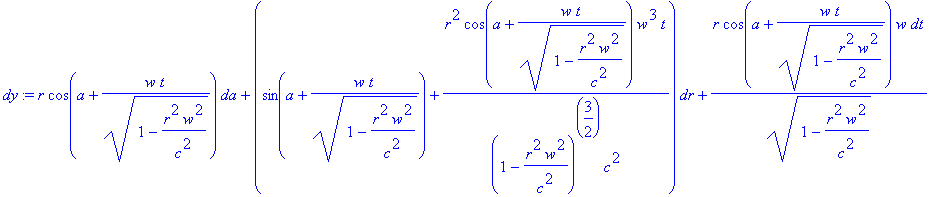
Дифференциал преобразования координаты z
> dz1:=diff(z1,a)*da + diff(z1,r)*dr + diff(z1,t)*dt + diff(z1,z)*dz;
![]()
Дифференциал интервала
Составляем из дифференциалов координат дифференциал интервала
> ds2:=c^2*dt1^2-dx^2-dy^2-dz1^2;
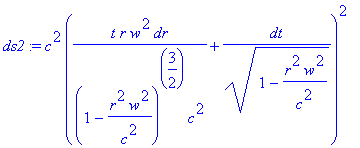
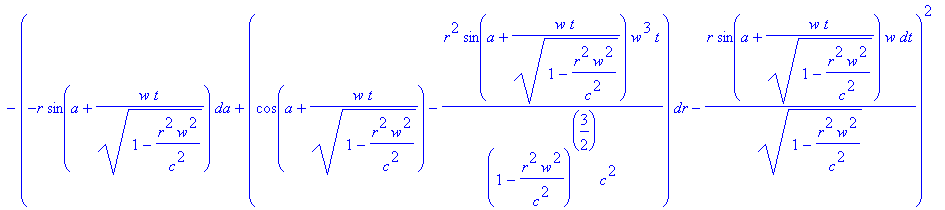
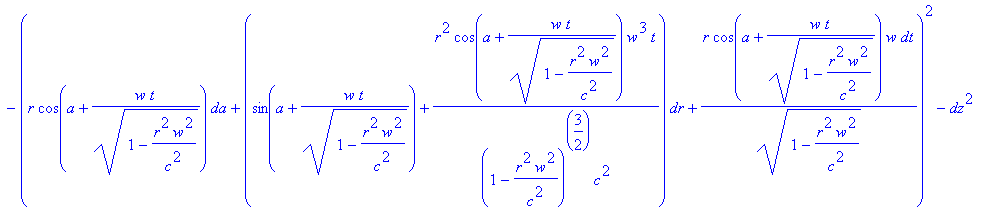
Упрощаем выражение
> ds2:=simplify(ds2);
![]()
![]()
![]()
Собираем коэффициенты
> ds2:=sort(collect(ds2,{da,dr,dt,dz}, distributed ),{da,dr,dt,dz});
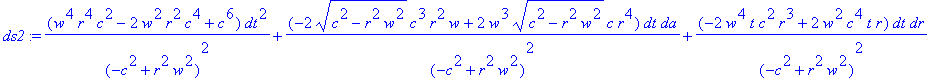
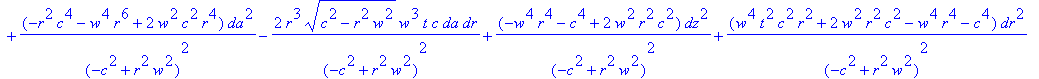
Расчет метрического тензора
Создаем двумерный массив 4 на 4 для хранения тензора
>
G:=array(1..4,1..4):
for i from 1 to 4 do
for j from 1 to 4 do
G[i,j] := 0;
end do;
end do;
Перебираем все члены полинома выше и, ориентируясь на дифференциальные множители раскоадываем по ячейкам массива
>
for n from 1 to nops(ds2) do
pwr := op(-1, op(n,ds2));
if nops(pwr) > 1 then
cmpn := op(n,ds2)/pwr;
pwr := op(1,pwr);
i := `if`( evalb(pwr = dt), 1, `if`( evalb(pwr = dr), 2, `if`( evalb(pwr = da), 3, 4 )));
j := i;
G[i,j] := simplify(cmpn);
print("В элемент " || i || ", " || j || " положено", G[i,j]);
else
pwr2 := op(-2, op(n,ds2));
cmpn := op(n,ds2)/pwr/pwr2;
i := `if`( evalb(pwr = dt), 1, `if`( evalb(pwr = dr), 2, `if`( evalb(pwr = da), 3, 4 )));
j := `if`( evalb(pwr2 = dt), 1, `if`( evalb(pwr2 = dr), 2, `if`( evalb(pwr2 = da), 3, 4 )));
G[i,j] := simplify(cmpn/2);
print("В элемент " || i || ", " || j || " положено", G[i,j]);
G[j,i] := simplify(cmpn/2);
print("В элемент " || j || ", " || i || " положено", G[j,i]);
end if;
end do;
![]()
![]()
![]()


![]()


![]()
![]()
![]()


![]()
![]()
![]()

Итоговый тензор имеет вид
> print(G);
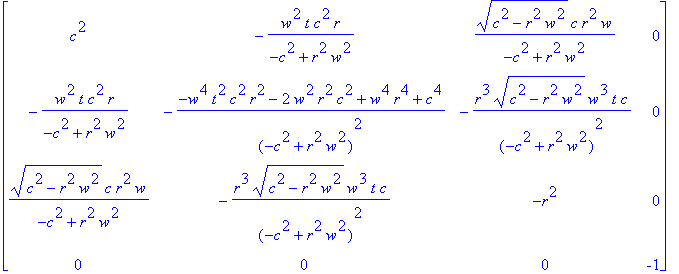
Пространственный метрический тензор
Заполняем компоненты пространственного тензора по формуле
>
GG:=array(1..3,1..3):
for i from 1 to 3 do
for j from 1 to 3 do
GG[i,j] := -G[i+1,j+1] + G[1,j+1] * G[i+1,1] / G[1,1];
end do;
end do;
Получается тензор
> print(GG);
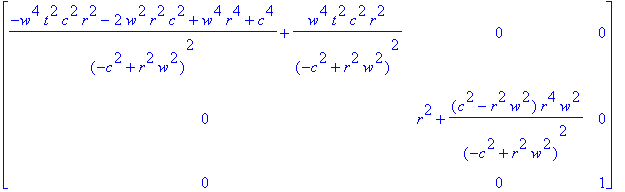
Расчет длины окружности
Вспомогательный вектор с дифференциалами
> dxx:=[dr,da,dz];
![]()
Освобождаем переменные для индексов, чтобы не мешались
> unassign('i','j');
Считаем сумму по первому индексу
> expr:=GG[1,j]*dxx[1]*dxx[j] + GG[2,j]*dxx[2]*dxx[j] + GG[3,j]*dxx[3]*dxx[j];
![]()
Рассчитываем квадрат бесконечно-малого пути
> dl2:=eval(subs(j=1,expr)+subs(j=2,expr)+subs(j=3,expr));
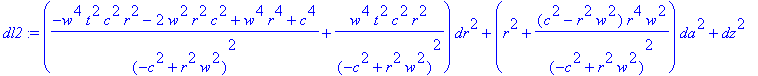
> dl2:=subs({dr=0,dz=0,r=R,w=V/R,da=1},dl2); assume(R>0);
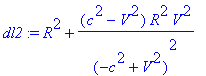
> dl:=sqrt(dl2);
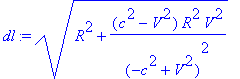
> simplify(int(dl,a=0..2*Pi));
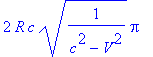
Домой | Мысли | Физ-мат Мысли | Наверх.